Random Vibration Testing

Any type of vibration is described by the time history of motion, where the amplitude of the motion is expressed in terms of displacement, velocity or acceleration.

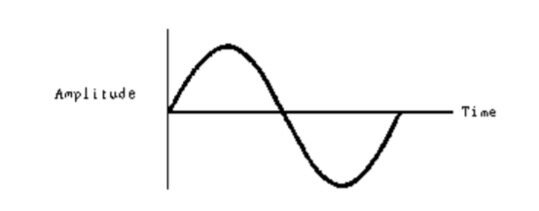
The simplest motion is sinusoidal vibration and can be fully described by straightforward mathematical equations. The below figure shows the amplitude time plot of a sinusoidal vibration and indicates that sinusoidal vibration is cyclic and repetitive. That is to say, if frequency and amplitude (or time and amplitude) are defined, the motion can be predicted at any point in time.

As opposed to sinusoidal vibration, a random vibration is one whose absolute value cannot be predicted at any point in time as there is no well defined periodicity – the amplitude at any point in time is not related to that at any other point in time.

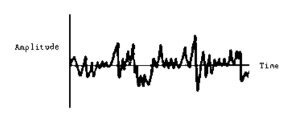
The below figure shows the amplitude time history of a random vibration where the lack of periodicity is evident.

Random vibrations are the oscillations of mechanical systems excited by environments that vary randomly in time and, perhaps, space. Practically all real physical systems are subjected to random dynamic environments, and many systems will fail due to the effects of these exposures. Mathematical and experimental studies of random vibrations are pursued to explain observed phenomena, to predict the characteristics of system responses, to aid in the design of mechanical systems, and to demonstrate the survivability of physical systems.

Random vibrations have been studied in a mathematical framework since about the turn of the previous century. Albert Einstein (1905) performed the first mathematical analysis that could be considered a random vibration analysis when he modeled the Brownian movement of particles suspended in a liquid medium.

Numerous studies whose results would later be used to explain the random vibration of mechanical systems were carried out in the decades to follow, but it was not until the 1950’s that the subject of random vibrations of mechanical systems would be addressed directly, with the approach in use, today. A comprehensive theory of random vibrations was needed to accurately predict structural response to jet engine noise and missile launch-induced environments.

In 1958 Steven Crandall organized a special summer program at the Massachusetts Institute of Technology to address problems in the various areas of random vibrations of mechanical systems. Specifically, the papers covered topics such as analysis of random vibrations and design for random environments, random vibration testing, and the analysis of data from random environments.

What is the difference between sinusoidal vibration and random vibration?

An important difference between sinusoidal vibration and random vibration is that for the random vibration, numerous frequencies may be excited at the same time. Hence structural resonances of different components can be excited simultaneously, the interaction of which could be vastly different from sinusoidal vibration, wherein each resonance would be excited separately.

Even if the instantaneous amplitude of a random vibration cannot be expressed mathematically as an exact function of time, it is still possible to determine the probability of occurrence of a particular amplitude on a statistical basis.

To characterize a stationary process, an ensemble of possible time histories must be obtained, in which the amplitude is measured over the frequency range of excitation.

Therefore, the three parameters of interest are: frequency, time and amplitude that will provide the ability to analyze a random process in a statistical sense.

The characterization of random vibration typically results in a frequency spectrum of Power Spectral Density (PSD) or Acceleration Spectral Density (ASD), which designates the mean square value of some magnitude passed by a filter, divided by the bandwidth of the filter. Hence, Power Spectral Density defines the distribution of power over the frequency range of excitation.

While the term Power Spectral Density PSD is commonly used to specify a random vibration event, ASD, Acceleration Spectral Density, is more appropriate when acceleration is being measured and used in structural analysis and testing.

A measurement of the Acceleration Spectral Density ASD is the usual way to specify random vibration. The root mean square acceleration Grms is the square root of the area under the ASD curve in the frequency domain. The Grms value is typically used to express the overall energy of a particular random vibration event and is a statistical value used in mechanical engineering for structural design and analysis purposes.

When your goal is avoiding mechanical failure and equipment malfunction, random vibration could be considered as either:

a) an infinite number of harmonic vibrations with unpredictable amplitude and phase relationships in the frequency domain; or

b) the sum of an infinite number of infinitesimal shocks occurring randomly in the time domain.

In the first case, the primary concern may be the response at a particular frequency.

For example, when a displacement sensitive device is excited at its natural frequency, relatively large displacements may result in malfunction. In such a case, the malfunction might be corrected by reducing the amplitude of excitation at the particular frequency of concern - the natural frequency of the device. This might be accomplished by inserting a vibration isolator between the source of excitation and the device or alternatively, displacement might be reduced by adjusting the stiffness of the device, or by increasing damping at the natural frequency of the device.

If the random vibration is considered as an infinite number of infinitesimal shocks, the overall Grms may result in a fatigue related structural failure of a component due to the intermittent shocks associated with the random excitation. In this case, the problem might be corrected by reducing the overall Grms or by increasing the strength of the component.

Types of Random Vibration

Random vibration can be broadband or narrow band. It can also be stationary or non-stationary. In addition, white noise and pink noise are two special cases of random vibration. And sometimes, measured data has a "sine-on-random" characteristic.

Let’s take an example from the automotive industry. Let’s consider that an automotive manufacturer is developing a GPS navigation system for its cars.

The GPS system will interface with a computer mounted underneath the dashboard and will have a display screen so that the driver can navigate to his/her destination.

The engine, transmission and aerodynamic effects are each sources of vibration, as such the navigation computer must be designed to withstand vibration. But the most dominant source of vibration is transmitted from the road, through the tires and suspension and into the vehicle chassis.

Of course, appropriate vibration test levels must be conducted.

Now, the automotive manufacturers are all tied to build their vehicles following standards and such, is searching for reference data in different standards available like MIL-STD-810E, SAE standards and others. While the manufacturer may find useful data, he will also realize that he must take field measurements to establish the maximum expected vibration level for his specific product.

To take field measurements, the manufacturer will mount accelerometers inside the test car near the navigation system mounting location, uses a data acquisition system to monitor the data and drives the car through a variety of roads including city streets and highways.

What data can he expect? What type of vibration? The data will likely show that vibration is random. An exception may occur if a particular frequency is excited and this will be resonant excitation and the natural frequency would have a sinusoidal time history response. But even so, the amplitude of the sinusoid may vary in a random manner. To keep it simple, consider that the response will be random vibration.

But will these random vibration “characteristics” vary with speed, road conditions, total vehicle weight or other variables? As this amount of variability will affect the amount of data which must be collected and analyzed.

A probable outcome is that the character of the random vibration may be reasonably consistent as the car travels at 60 mph on a particular highway and on the other hand, the character could vary considerably as the vehicle experiences stop-and-go driving over a city street filled with potholes or railroad tracks and construction detours.

When a Random Vibration is stationary or nonstationary?

In terms of its statistical properties, consider that random vibration can be characterized such as mean value, standard deviation, and kurtosis.

The random vibration is "stationary" if these statistical properties remain constant with time. If not, it is "nonstationary." Stationary vibration is an idealized concept but all vibrations are ultimately nonstationary. But still, certain types of random vibration may be regarded as reasonably stationary.

Let’s see an example of stationary and nonstationary random vibration.

Remember the vehicle from the previous example? When the car travels at a constant speed of 60 mph down a flat interstate highway, experiences stationary vibration, or at least the vibration is stationary as long as the vehicle remains under those conditions. However, the vehicle experiences a series of transient vibration events during the stop-and-go city driving or while it crosses railroad tracks, encounters potholes and other obstacles. Transient vibration is nonstationary.

Random Vibration Testing

A random vibration test is a test that simultaneously sends random vibrations that over time include the entire vibration test’s frequency range.

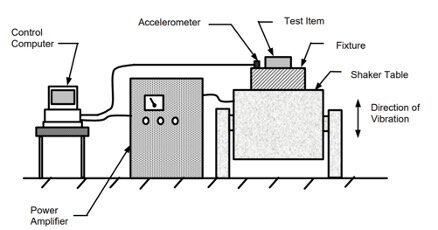
Electronic and mechanical components may be mounted on an electromagnetic shaker table for the purpose of random vibration testing.

The shaker provides a base input to the test item. A control computer applies a random vibration signal to the shaker via a power amplifier. The shaker applies mechanical vibration to the test item.

The shaker vibration is monitored by accelerometers. The accelerometers provide a feedback signal to the control computer, as shown below:

When should you use Random Vibration Test?

Vibration test engineers should use random vibration testing when:

looking to simulate vibration experienced by components and assemblies used in automobiles, electronics, military vehicles, aircraft and space vehicles
looking to stimulate of latent parts and workmanship defects
looking to replicate field measurements, “real-life” situations
looking for production testing, stress screening and prototype testing
looking for product qualification to MIL-STD, DIN, ISO, IEC and other standards

Why should you use Random Vibration Test?

Random vibration testing is beneficial for multiple reasons:

The “real-world” is less synthetic than a single sine wave. Exciting all the frequencies makes a random test a more realistic representation of what occurs in the “real-world”.
A random test can be created to represent multiple environments under which the item to test may be used in the “real-world”
A random test can be accelerated to create a test representative of a longer field life than may be practically run in a laboratory
A DUT may have multiple resonances. Sine testing can only test one resonance at a time and cannot test the interactions of multiple resonances. By exciting all resonances at the same time, random vibration gets a glimpse of the interaction between these multiple resonances.

Reduce the risk from the start

By working with a testing laboratory who has an expert understanding of the environment in which you are looking to operate, you can reduce the risk of product failure early on, starting from the designing stage. We can help you achieve this in various ways, including computer simulation by Finite Element Analysis during the design phase, and engagement with our specialized team to ensure that the optimum vibration testing conditions are selected. Commercial, Military and Aerospace standards we commonly test to include IEC 60068, ASTM D4728, IEC 61373, MIL-STD 810, MIL-STD 883, MIL-STD 202, MIL-STD 167 and MIL-PRF 28800 and can take care of your complete testing process to meet unique, bespoke, or complex project requirements.

Testing & Calibration Inquiry